Estudo Dirigido - Método de Newton-Raphson

Leitura Recomendada:  

Leitura Complementar:  

Estudo dirigido sobre Método de Newton-Raphson, com Aplicação, podendo ser entregue até 26/11/04. O assunto fará parte da matéria da Avaliação Global.

O Método de Newton-Raphson é a técnica usada por muitos programas de computadores comerciais e científicos para aproximar as raízes de uma equação. Devem ser observadas as hipóteses adotadas para a implementação analítica do método e sua interpretação geométrica, que facilita o entendimento da natureza iterativa do método. Importante também observar as situações em que  método falha, buscando entender as condições para sua utilização.

Método de Newton - Implementação analítica

Leitura: 
Seção: 6.4: Método de Newton (pg. 363 a 364) (Anton).

O método de Newton é dado pela expressão (4). Observe que o procedimento é iterativo, ou seja obtém-se uma fórmula que calcula cada aproximação aperfeiçoada a partir da aproximação precedente. Os valores das derivadas nestes diversos pontos são utilizados para produzir uma seqüência de pontos que convergem rapidamente para a raiz desejada. Entenda mais facilmente o funcionamento do método através de sua interpretação gráfica.

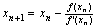(4)

Antes de passar à implementação computacional, faça manualmente os exemplos 1 e 2 de maneira a compreender o mecanismo do método. Podemos conclui que se duas aproximações sucessivas forem iguais, temos então uma aproximação para um zero da equação.

Observe sempre se as hipóteses do método estão atendidas:

  1. Exista apenas uma raiz no intervalo [a, b], onde se deseja obter a raiz
  2. As derivadas primeira e segunda são não-nulas e preservam o sinal no intervalo de pesquisa da raiz. 
  3. A derivada da função no ponto xn é diferente de zero (f'(xn)¹0).

Método de Newton - Implementação computacional

Leituras: 
Seção 6.5.1: Método de Newton (F. F. Campos)

É apresentado um algoritmo para o cálculo de uma raiz pelo Método de Newton, podendo ser utilizado em qualquer linguagem. Os parâmetros de entrada são o valor inicial, a tolerância para o cálculo da raiz e número máximo de iterações. A função f(x) e sua derivada f'(x) devem ser especificadas de acordo com a linguagem de programação utilizada.

Os parâmetros de saída são a raiz, o número gasto de iterações e a condição de erro, indicativo que a raiz não foi encontrada com a tolerância e o número máximo de iterações fornecidos.

Implemente o algoritmo e proceda sua validação através dos exemplos 6.29 e 6.30. Utilize os mesmos parâmetros de entrada fornecidos pelo autor e verifique se as respostas que você obteve são compatíveis.

Observe a propriedade de convergência quadrática, significando que nas proximidades da raiz, o número de dígitos corretos da estimativa da raiz praticamente dobra a cada iteração.

Algumas dificuldades com o Método de Newton

Leituras: 
Seção: 6.4: Algumas dificuldades com o Método de Newton (pg. 364) (Anton).

Quando funciona o Método de Newton, as aproximações convergem para a solução com grande velocidade.

Há situações, porém, nas quais o método falha:

Caso deseje, consulte livros de análise numérica (alguns foram recomendados!) e saiba mais sobre as condições de convergência do Método de Newton e para uma discussão sobre erros.

Outras considerações sobre o Método de Newton

O método de Newton é um dos processos numéricos utilizados para aproximar soluções de equações e foi desenvolvido por Isaac Newton no século dezessete. 

Se sua escolha inicial de x0 não for suficientemente próxima do zero desejado, é possível que você obtenha aproximações para um outro zero. Assim, quando você for aplicar o método de Newton, você deverá fazer um rápido esboço do gráfico da função para obter sua aproximação inicial.

Em suma, quando você for aplicar o Método de Newton para resolver uma equação da forma f(x) = 0, siga os seguintes passos:

  1. Escolha adequadamente a primeira aproximação x0. Um esboço rápido do gráfico de f irá ajudá-lo a obter uma escolha razoável.
  2. Com o valor de x0 na fórmula (4), obtenha uma segunda aproximação x1. Então, use x2 em (4) a fim de obter uma terceira aproximação x2, e assim por diante, até que xn=xn-1 com a aproximação desejada.

Aplicação

Implementação

Implemente algoritmo do método de Newton-Raphson na linguagem de sua preferência.

Exercícios

Observações

  1. Apresentar os exercícios resolvidos, o algoritmo implementado e a linguagem utilizada
  2. Valor da avaliação: 8 pontos.
  3. O Estudo Dirigido pode ser efetuado em duplas.
  4. Data de Entrega: 26/11/04.

Links Interessantes